鋼結(jié)構(gòu)技術(shù)論文

鋼結(jié)構(gòu)技術(shù)論文
- 深圳機場:異型曲線立體桁架制造技術(shù)
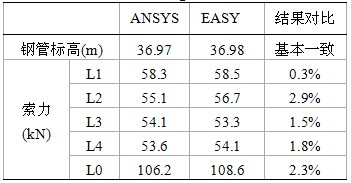
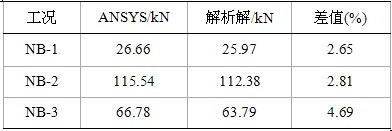
- 自平衡魚腹式索鋼架混合結(jié)構(gòu)支撐體
- 基于FDS溫度場的大空間網(wǎng)架結(jié)構(gòu)火災(zāi)
- 深圳證交所大廈動力彈塑性分析
- 巨型玉璧內(nèi)圓上部懸掛結(jié)構(gòu)安裝技術(shù)
- 高聳避雷塔抗風分析研究與優(yōu)化設(shè)計
- 貴陽漁安中天文化活動中心鋼結(jié)構(gòu)設(shè)
- 貴陽市城鄉(xiāng)規(guī)劃展覽館結(jié)構(gòu)設(shè)計
- 薄壁方鋼管梁柱加腋節(jié)點數(shù)值分析
- 萊蕪銀山型鋼3號高爐鋼結(jié)構(gòu)工程吊裝
- 大跨度門式剛架在工程中的應(yīng)用










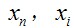
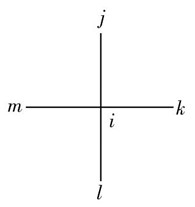
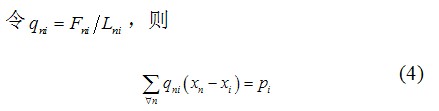
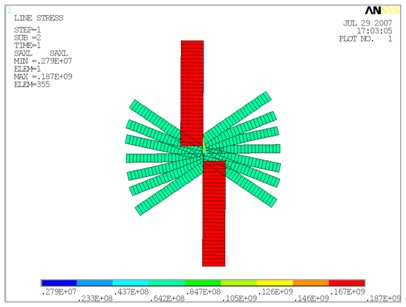
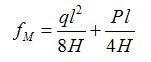 (
(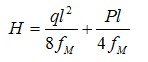 (
(
 :
: 